Articles & Videos
Developing creative and lateral thinking skills in maths
Categories
Subscribe to our newsletters
Receive teaching resources and tips, exclusive special offers, useful product information and more!
Developing creative and lateral thinking skills in maths
BitMaths 22/2/24

When solving abstract or rehearsed mathematical problems, students need to recall and apply the rules and procedures they have practised in class. However, when it comes to solving unrehearsed real-world problems, students need to make a leap into the unknown and think on their feet. For this reason, it’s important for students to learn how to think creatively. One way to do this is to develop lateral thinking skills.
Lateral thinking is the ability to solve problems by thinking outside the box and tackling problems in unique and innovative ways. It encourages the mind to be flexible, which makes it easier to bridge the gap between content knowledge and new contexts.1 2
Here are four ways to encourage and support creative and lateral thinking in maths lessons.
Use inquiry in teaching
Using well-guided constructive questions in teaching promotes creative and agile thinking. It requires students to think logically as they try to connect prior learning to new situations, resulting in more meaningful and engaging learning. 3 4
For example, asking students to explain why 34 is equal to 81, not 12, encourages students to think and take an active role in their learning, which is more powerful and effective than simply telling students that 34 = 81.
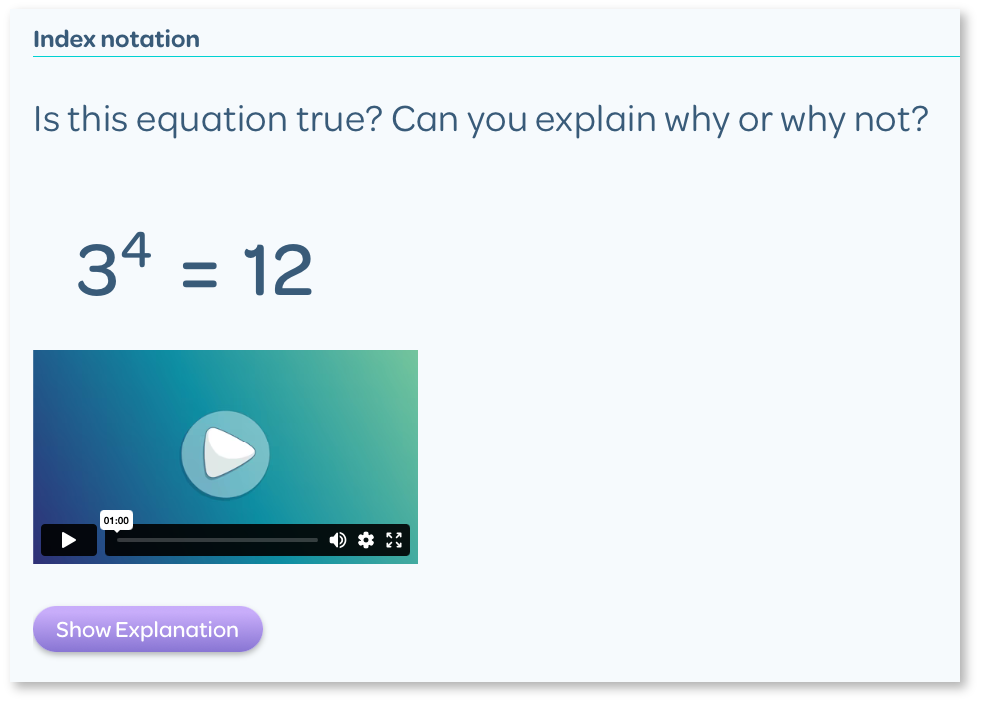 Example of an open-ended question from BitMaths: NA702 Index Notation (Australian Curriculum; Victorian Curriculum).
Example of an open-ended question from BitMaths: NA702 Index Notation (Australian Curriculum; Victorian Curriculum).
Throughout BitMaths teachers are prompted to constantly ask students ‘Why do you think this happens?’ before explaining the how.
 Example of an answer from BitMaths: NA702 Index Notation (Australian Curriculum; Victorian Curriculum). Answers in BitMaths can include a written answer, a video and a ‘remember’ note to help explain the answer process.
Example of an answer from BitMaths: NA702 Index Notation (Australian Curriculum; Victorian Curriculum). Answers in BitMaths can include a written answer, a video and a ‘remember’ note to help explain the answer process.
Set novel problems
To help students to think creatively, try using novel problems in class: outside-the-box thinking questions that require students to find a solution to a unique or unconventional problem.
For example, ask students to measure the length of a classroom without using typical measuring devices or standard units of measurement. This requires students to create their own measuring device or form of measurement.
To support students with a novel problem, encourage them to persevere on their own or to partner with a classmate. It’s important to give students an opportunity to find a breakthrough on their own. Even if their thinking does not result in a viable solution, any thinking that leads to a solution is valuable.

Example of a novel problem from BitMaths: NA802 Operations with Integers and Fractions (Australian Curriculum; Victorian Curriculum), NA404 Operations with Integers and Fractions (NSW Syllabus).
Model a variety of ways to solve problems
To help students recognise that a maths problem can be solved using more than one method, teach the same piece of content in different ways.
For example, when we demonstrate how to find 10% of 40 using three different methods – mental shortcuts, multiplying fractions and using a calculator – we invite students to consider the different methods and select their favourite. When faced with a problem-solving task, this encourages students to take ownership of the problem and find their own way of solving it.
Encouraging students to use different methods to solve problems helps them to see solution options when approaching new problems and to find efficient strategies that align with their way of thinking.
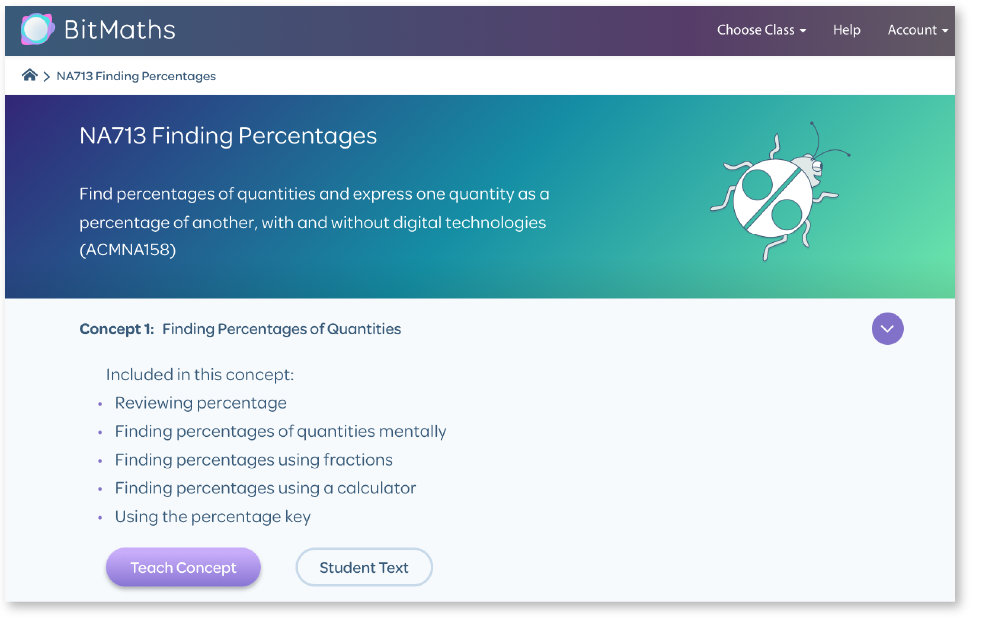 Example of the different teaching methods used to find percentages from BitMaths NA713 Finding Percentages (Australian Curriculum; Victorian Curriculum), NA413 Finding percentages (NSW Syllabus).
Example of the different teaching methods used to find percentages from BitMaths NA713 Finding Percentages (Australian Curriculum; Victorian Curriculum), NA413 Finding percentages (NSW Syllabus).
Always discuss alternative solutions
Discussion is a simple and effective tool to introduce students to alternative thinking pathways. When solving a mathematical problem as a class, always encourage students to explain the method they used to solve the problem. This provides students with an opportunity to articulate their own thinking while also relating their solutions to their classmates’ solutions and understanding of the problem.
By discussing solutions, we help students make more connections between the content and real-life situations and equip them with skills to use when facing unrehearsed problems.
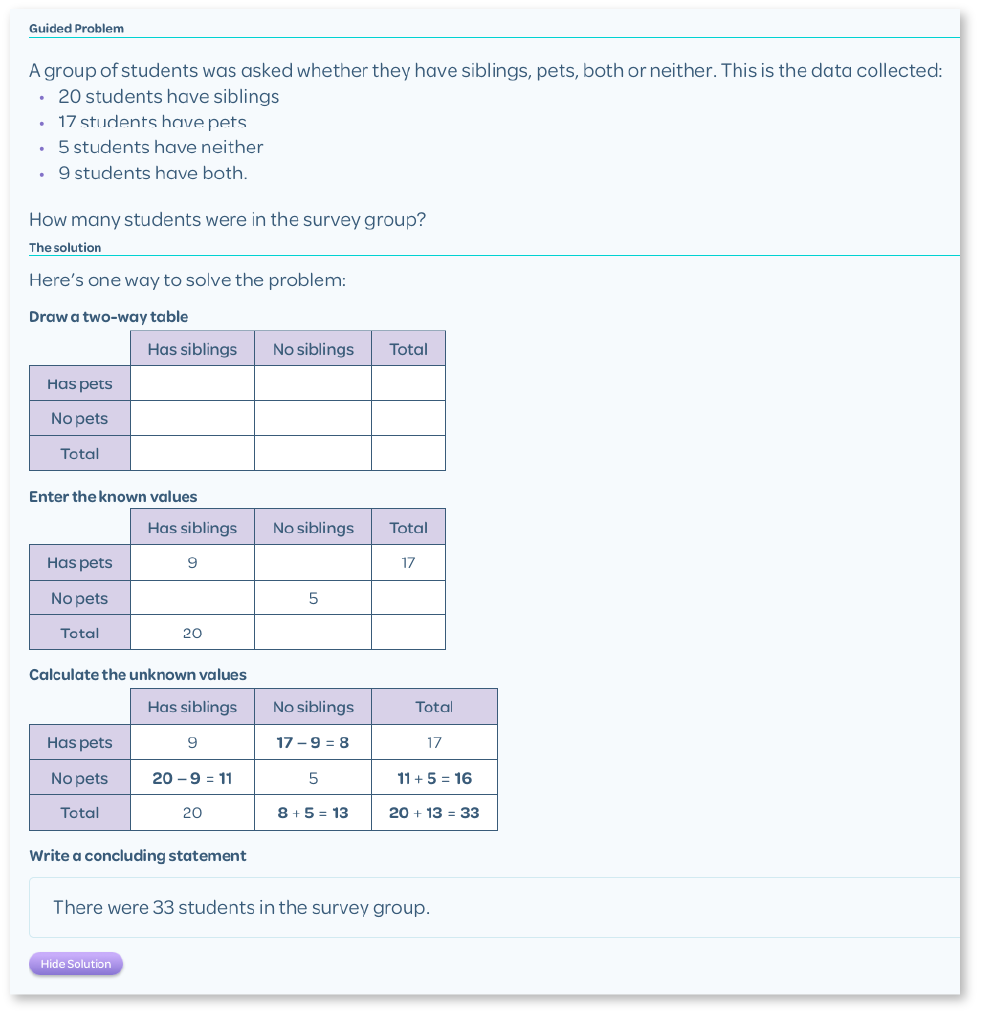 Example of a guided problem from BitMaths: SP803 Venn Diagrams and Two-way Tables (Australian Curriculum; Victorian Curriculum), SP414 Venn Diagrams and Two-way Tables (NSW Syllabus).
Example of a guided problem from BitMaths: SP803 Venn Diagrams and Two-way Tables (Australian Curriculum; Victorian Curriculum), SP414 Venn Diagrams and Two-way Tables (NSW Syllabus).
Creative and lateral thinking are just two of the valuable skills embedded in the BitMaths program. There’s so much more to discover. Request a free trial today and explore for yourself!
References
de Bono, E 2014, ‘Creative and Lateral Thinking’, Encyclopaedia of Educational Theory and Philosophy, 187–189. Available at: http://dx.doi.org/10.4135/9781483346229.n86.↩
Plucker, JA, Runco, MA & Hegarty, CB 2011, ‘Enhancement of Creativity’, Encyclopaedia of Creativity, 2nd Edition, 456–460. Available at: https://doi.org/10.1016/B978-0-12-375038-9.00090-X.↩
Australian Curriculum, Assessment and Reporting Authority 2024, Inquiry-based learning. Available at: https://www.education.gov.au/australian-curriculum/national-stem-education-resources-toolkit/i-want-know-about-stem-education/what-works-best-when-teaching-stem/inquiry-based-learning.↩
Kuhlthau, CC, Maniotes, LK & Caspari AK 2015, Guided Inquiry: Learning in the 21st Century, 2nd Edition, Bloomsbury Publishing Plc.↩