Back to Games & Activities articles & videos

How Maths Trek aligns with Peter Sullivan’s research-informed strategies for effective maths teaching

Maths Trek 22/10/25

With increased importance being placed on the science of learning, more educators are making greater efforts to ensure their teaching aligns with current research and best practice pedagogy. So when staff at Perth’s Whitford Catholic Primary School made the decision to implement a consistent, whole-school maths program, they knew their chosen resource would need to correspond with key research.

During their decision making process, they consulted Professor Peter Sullivan’s six research-informed strategies for effective maths teaching detailed in his 2011 paper published by the Australian Council for Educational Research (ACER).

These principles are:

1. Articulating goals
2. Making connections
3. Fostering engagement
4. Differentiating challenges
5. Structuring lessons
6. Promoting fluency and transfer

When reviewing resource options to align with these principles, Whitford staff found that, while other maths programs addressed five of the six key principles, Maths Trek was the only one that also met the sixth principle, ‘Promoting fluency and transfer’. For this reason, Maths Trek was the logical and standout choice.

In Sullivan’s sixth principle, he emphasises the importance of fluency and how it can be developed in two ways: by short everyday practice of mental processes; and by practice, reinforcement and prompting transfer of learnt skills¹.

So let’s unpack the two components of this principle and find out how Maths Trek fits the bill.

Part 1: Short everyday practice of mental processes

This first part of the principle highlights the importance of providing opportunities for students to develop mental fluency. While there are naturally many opportunities within a maths program to foster and develop fluency, Maths Trek’s Daily Number Practice tool is specifically designed to focus on fluency development through quick daily practice of mental computation. Teachers can either display this digital tool from within the Maths Trek online teaching resources, or have their students access it independently through the Maths Trek student site. Unique questions are generated every time a student starts a new set to allow for continued fluency practice, and immediate feedback is given when an answer is entered.

For more information on Daily Number Practice read our detailed article or to see how the tool works, check out the video below: Feature Spotlight: Maths Trek’s Daily Number Practice.

Part 2: Reinforcement and prompting transfer of learnt skills

The second part of the principle calls for the need for spaced and interleaved practice. Traditionally in education, maths has been delivered in grouped (sometimes referred to as chunked) units with a focus on one concept at a time. For example, a Year 4 teacher may deliver a three-week unit on fractions before administering a summative assessment, and then moving on to the next unit.

By comparison, Sullivan’s sixth principle advocates for a method called spaced retrieval practice². In this approach, the same Year 4 teacher would teach a lesson on fractions, then in the next lesson move on to a complementary concept such as quarter and half turn rotations in tessellating patterns, which requires prerequisite fractions knowledge. This prompts students to retrieve and apply their skills from the first lesson alongside like-concepts for maximum retention and application. Later, the teacher would revisit the initial learning on fractions, but with increased complexity. The space between the original lesson and the subsequent fractions lesson is proven to assist in increased student retention, as opposed to traditional grouped units of work where a concept may only be taught once in the year or isn’t revisited for extended periods of time.

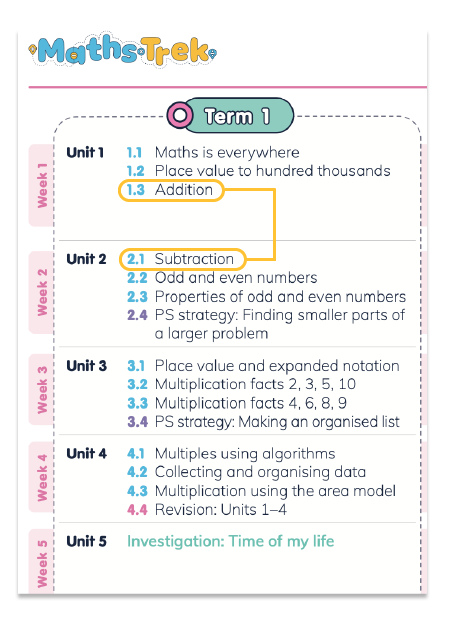
Spaced retrieval practice uses the principles of cognitive science to help students consolidate their learning in long-term memory, so they retain the information for longer and are better able to apply their learning in the future³. Maths Trek’s Scope and Sequence has been carefully designed to follow this approach to align with best practice teaching, reinforcing concepts and prompting transfer of learnt skills across topics throughout the year. Here’s an example from the Maths Trek 4 Yearly Plan:

In Unit 1.3 (as highlighted below), students learn about addition and are explicitly taught how to add three-digit numbers with regrouping. This is immediately followed by its related operation, subtraction, in Unit 2.1. These skills are further practised in subsequent topics until they are revised a few weeks later in the revision unit. This is quickly followed by applying the concept to real-world contexts in the investigation and then finally assessed.

This spaced learning approach is repeated each term across the year where the teaching of addition increases in complexity, before being practised, revised, applied and assessed.

The importance of this pedagogical approach is echoed in other research, including the analysis paper The Science of Maths and How to Apply It which states that spaced practice is likely to yield better results than content which is presented in a block⁴.

Sullivan’s principles in action

The staff at Whitford Catholic Primary School hold Sullivan’s research in high regard and commend the way Maths Trek reflects his recommendations. They believe Maths Trek ‘revisits concepts to embed knowledge’ and that the ‘linking of topics across contexts’ is a standout aspect of the program. After six months using the program, the staff reported ‘deeper learning and increased retention’ amongst students, as well as a higher level of engagement with the subject.

It’s clear that Maths Trek’s comprehensive structure and focus on fluency really shines, giving teachers the confidence and tools to ensure all aspects of effective teaching in mathematics are met.

Ready to explore Maths Trek with your school? Browse our website to find out more about the program features, sign up for a free trial to explore the resources firsthand or schedule a professional learning workshop for your school.

References

1. Sullivan, P. (2011) ‘Teaching Mathematics: Using research-informed strategies’, Australian Council for Educational Research, Australian Education Review no. 59 Available at: https://research.acer.edu.au/cgi/viewcontent.cgi?article=1022&context=aer↩

2. Mathematics Hub (no date) ‘Teaching strategies’, Education Services Australia. Available at: https://www.mathematicshub.edu.au/plan-teach-and-assess/teaching/teaching-strategies/↩

3. Practice guide (2021) ‘Spacing and retrieval practice: Improve students’ long-term retention of learning’, Australian Education Research Organisation (AERO). Available at: https://www.edresearch.edu.au/sites/default/files/2021-09/tried-tested-spacing-retrieval-practice-aero.pdf↩

4. Merlo, S. (2024) ‘The Science of Maths and How to Apply It’, The Centre for Independent Studies, Analysis Paper 71. Available at: https://www.cis.org.au/publication/the-science-of-mathematics-and-how-to-apply-it/↩

More Maths Trek articles & videos

Maths Trek

Maths Trek Online: Virtual Tours

Maths Trek

Grattan Institute: ‘1 in 3 Australian school students fail to achieve proficiency in maths’